Buongiorno
Nella lezione di Analisi Matematica 1 (2010 - 2011) Lezione AM11_L028 - Definizione di derivata (come limite del rapporto incrementale ed in termini di o piccolo). Derivata di alcune funzioni elementari.
L'interpretazione geometrica di O piccolo permette di avere un'idea più chiara per una approssimazione con una reta (Grado 1 del polinomio.). è possibile avere analogamente un rapresentazione geometrica per un polinomio di grado maggiuore di 1? Grazie.
O piccolo, interpretazione geometrica
Re: O piccolo, interpretazione geometrica
Provo a rispondere. Il polinomio di Taylor di ordine 1 approssima la funzione con la sua retta tangente in un punto. Matematicamente significa che la differenza tra la funzione e la retta tangente diventa piccola a piacere a patto di calcolarla in un punto abbastanza vicino a quello scelto per lo sviluppo. In termini più pratici se immagini di fare lo zoom della funzione nell' intorno di un punto, man mano che ingrandisci, questa assomiglierà sempre di più alla sua retta tangente, fino a confondersi con essa. Anche la terra, la cui superficie non è piana, vista dalla nostra prospettiva può essere approssimata con il piano tangente ( che è l' analogo della retta tangente in due dimensioni). Quello che riusciamo a vedere noi è in fondo un piccolo intorno di un punto della terra ed è per questo che ci sembra piatta, perché è approssimata bene dal suo piano tangente.
Se riduci lo zoom la funzione potrebbe cominciare a discostarsi sempre di più dalla retta tangente, perché magari ha una curvatura. Se vuoi continuare ad approssimare "abbastanza bene" la funzione in un intorno un pò più grande non ti basta più una retta ma devi prendere una curva. Nel polinomio di ordine due ( se la derivata seconda della funzione non è zero ) questa curva è una parabola. Significa che abbastanza vicino al punto in cui sviluppi la funzione questa si confonde con una parabola, la cui equazione è data appunto dal polinomio di Taylor di ordine due. La parabola ti permette magari di approssimare la funzione in un intorno un pò più grande di quello della retta, hai bisogno cioè di meno zoom per confondere la funzione con la parabola data dal polinomio di ordine 2. Usando il polinomio di ordine tre ( se la derivata terza della funzione non è zero ) hai una situazione analoga, solo che questa volta non stai approssimando la funzione con una parabola, ma con una cubica, ovvero una curva nel piano che ha come equazione un polinomio di grado 3. La cubica seguirà ancora più fedelmente la funzione, magari in un intorno ancora più grande ( hai cioè bisogno di ingrandire meno per confondere la funzione con il suo polinomio di grado 3). Situazione analoga con i gradi successivi: Data una funzione, scegli un punto e vicino a quel punto approssimi la funzione con una curva che ha come equazione un polinomio di grado k. Se ingrandisci abbastanza la funzione questa tenderà a confondersi sempre di più con tale curva ( il suo polinomio di ordine k). Anche se in generale non è del tutto vero, puoi pensare che maggiore è il grado del polinomio maggiore sarà il suo grado di approssimazione. Se hai ancora dei dubbi chiedi pure! magari non sono stato abbastanza chiaro!
Se riduci lo zoom la funzione potrebbe cominciare a discostarsi sempre di più dalla retta tangente, perché magari ha una curvatura. Se vuoi continuare ad approssimare "abbastanza bene" la funzione in un intorno un pò più grande non ti basta più una retta ma devi prendere una curva. Nel polinomio di ordine due ( se la derivata seconda della funzione non è zero ) questa curva è una parabola. Significa che abbastanza vicino al punto in cui sviluppi la funzione questa si confonde con una parabola, la cui equazione è data appunto dal polinomio di Taylor di ordine due. La parabola ti permette magari di approssimare la funzione in un intorno un pò più grande di quello della retta, hai bisogno cioè di meno zoom per confondere la funzione con la parabola data dal polinomio di ordine 2. Usando il polinomio di ordine tre ( se la derivata terza della funzione non è zero ) hai una situazione analoga, solo che questa volta non stai approssimando la funzione con una parabola, ma con una cubica, ovvero una curva nel piano che ha come equazione un polinomio di grado 3. La cubica seguirà ancora più fedelmente la funzione, magari in un intorno ancora più grande ( hai cioè bisogno di ingrandire meno per confondere la funzione con il suo polinomio di grado 3). Situazione analoga con i gradi successivi: Data una funzione, scegli un punto e vicino a quel punto approssimi la funzione con una curva che ha come equazione un polinomio di grado k. Se ingrandisci abbastanza la funzione questa tenderà a confondersi sempre di più con tale curva ( il suo polinomio di ordine k). Anche se in generale non è del tutto vero, puoi pensare che maggiore è il grado del polinomio maggiore sarà il suo grado di approssimazione. Se hai ancora dei dubbi chiedi pure! magari non sono stato abbastanza chiaro!
Re: O piccolo, interpretazione geometrica
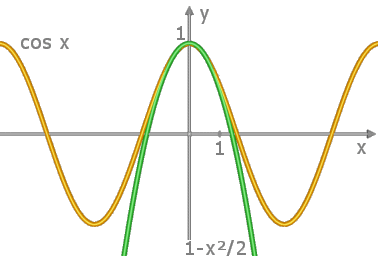
Guarda per esempio questa immagine. Puoi vedere che vicino al punto 0, la funzione si confonde molto bene con una parabola, quella data dal suo polinomio di taylor di ordine 2. Questa parabola approssima bene la funzione vicino a 0. Quanto vicino dipende ovviamente dal grado di approssimazione richiesto, ma penso che l' immagine renda l' idea
Re: O piccolo, interpretazione geometrica
Geometricamente, più alto è il grado, più la curva approssimante "aderisce" alla funzione su un intervallo più ampio attorno al punto.

